Origami Design: A Fuzzy Boundary Between Art and Science
Ever since I could read words on a page, origami has been everything from a pleasant past-time to a passionate preoccupation for me. It started with my amazement at friends who could take scraps of paper and turn them into cranes or balloons or canoes with what seemed like a few simple folds. Pretty quickly my curiosity got the best of me, and I dove headfirst into a few beginners’ books. I began by learning the language of origami with phrases like mountain fold, valley fold, reverse fold, pleat, crimp, squash fold, open sink, closed sink, etc. Then, I started small, learning first how to make traditional origami models such as the crane, boat, and swan.
After a few years, my age and education gave me the tools to research and find more complex origami models that I could attempt to create. What I found when I began researching modern origami artists still has me in awe. Artists such as Michael G. LaFosse, Robert J. Lang, Eric Joissel, Satoshi Kimaya, Brian Chang, and many others elevated origami from simple traditional to complex contemporary with models requiring square paper up to 9 feet in length (Michael G LaFosse’s crocodile shown below requires a 6 ft square piece of paper) [5]. All of a sudden, origami had become a design-rich, geometrically-ambitious art form. In the last few decades, it has become more than just a traditional Japanese art as engineers have transformed it into a technological tool.
Fig. 1 Alligator by Michael G. LaFosse [5]
Origami Design: Science or Art?
Origami is an ancient Japanese art form which had its roots over a thousand years ago in ancient Japan. Only in the last century’s intellectual revolution has it transformed into a more scientific and fully developed art form. Starting in the mid-twentieth century, origami master Akira Yoshizawa transformed the art of origami by increasing the complexity of origami and introducing new methods for folding paper.
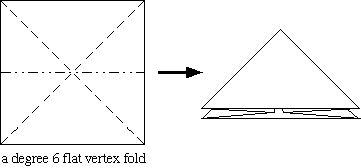
Shortly following Yoshizawa’s breakthroughs, origamists began to develop more mathematical methods for folding. Very quickly, it became a subfield of geometry with its own established theorems. One of the more simple theorems, Maekawa’s theorem, states that at any vertex where creases intersect in a flat crease pattern, the difference between the number of mountain and valley folds is always two (see diagrams below for examples) [1].
Fig. 2-3 Maekawa’s Theorem as shown by Tom’s Combinatorial Geometry Class – the regular dotted line represents a valley fold and the irregular represents a mountain fold. A vertex is where the lines (creases) intersect [3]
With Maekawa’s theorem as a prime example, origami design is a world filled with constraints. The designer, traditionally, is limited to a single square sheet of paper with no cuts, and no glue. This makes modern advanced origami models a modern feat of science that I’m sure most, if not all, of us may struggle to understand at first. Nonetheless, Satoshi Kamiya’s Ryujin 3.5 origami dragon majestically illustrates how one can still achieve brilliant design even within the bounds of very specific constraints.
Fig. 4 Ryujin 3.5 by Satoshi Kamiya [6]
In his revolutionary book, Origami Design Secrets, artist Robert J. Lang sets out to describe the process of designing a complex origami model without breaking any of the basic rules of origami. Lang describes design as follows: “I don’t think of origami design as a cookbook process so much as a bag of tricks from which I select one or more in the design of a new model” [2]. The variance that can be seen in origami design styles is directly related to the differences in that so-called bag of tricks. Throughout the book, he provides many examples of his own tricks or strategies to use as one is designing an origami model; however, he remarks that in the world of design, everyone has their own different tricks and strategies they have developed through their own experimentation. As we design, we can borrow from others’ ideas, but we need to also be mindful that innovation comes through trying to approach a problem differently.
On a more artistic note, Robert J. Lang illustrates that there are many little details that can make a huge difference in the end result of an origami model fold. One such example is the difference between hard and soft folds. Hard folds are ones in which the paper is creased thoroughly and with force. Too many folds like this can wear away the paper and cause it to tear in places. Soft folds, on the other hand, are only partial folds of the paper. Often, the correct combination of the two gives the model life and character. An elephant is a great example of this. If we think for a second about what an elephant looks like, our mind envisions a very rounded shape. If one were to fold an origami elephant with only hard folds, it would look stiff and lifeless. When soft folds are incorporated; however, it reminds us more of an elephant because its lines are less harsh. Then, the elephant comes to life [2].
Fig. 5 African Elephant, Opus 322 by Robert J. Lang [2]
Thus, we see origami under scrutiny as an art form, and as a scientific and mathematical method of design. In any design, it is important to see from both angles.
Modern Origami Technologies
In recent decades, many scientists have attempted to make large products collapsible into much more compact shapes for portability purposes. One very simple example of this is the modern umbrella. Recently, umbrellas have been made so that they can collapse small enough to fit into a handbag or back pocket. In this example and many others, origami design techniques help to provide the best solutions. Thankfully, because of recent developments in the mathematics and science behind this ancient art, engineers are able to use mathematical methods to design technological masterpieces.
At Brigham Young University, such Origami inspired mechanisms are being developed by the Compliant Mechanisms Research Team. Mechanisms (mechanical devices used to transfer or transform motion, force, or energy, typically using links and pin joints to achieve motion) designed using origami techniques can be quickly prototyped just using paper. Then, when the design has been perfected, it can be made in plastic, wood, cloth, or other materials to create the final product.
One such mechanism that the team has researched extensively is deployable structures. Working in tandem with NASA’s Jet Propulsion Laboratory, a few students, faculty, and origami artist Robert J. Lang teamed up in the design of a satellite solar array which can be folded into a compact shape during liftoff, later unraveling once space deployment has successfully taken place. This project is a significant development in satellite deployment as it significantly decreases the cost of launch [4]. This development has been exciting to many scientists considering that the techniques applied to this solar array can be applied to so many other designs in the future. Any future technology which may require a large surface area to be made compact could use these same strategies in development.
Fig. 6 Origami Solar Array Tile prototype designed by the compliant mechanisms team at Brigham Young University [4].
Because of its versatility and many applications, origami may one day become a common technique used in biomedical, aeronautical, and a host of other engineering design fields.
Conclusion
Not everyone who reads this will dive headfirst into the world of origami design; however, there are a few design lessons we can learn from this mathematical art. First, methods and technologies which have remained the same for many years can still change. It took origami multiple centuries before it finally blossomed into the incredible artistic examples shown above. Second, constraints do not put a cap on results. Many hundreds of awe-inspiring origami models have been developed within the constraints of traditionally origami by using mathematics and other tools to create. Finally, design is not always about checking off all the boxes. It’s about creating something that will serve a purpose with style. The soft-folded life-like elephant will always win against the box-checking lifeless elephant. Origami is not just an art form, nor is it just a science. It is a method of design.
References
[1] https://mathworld.wolfram.com/MaekawasTheorem.html
[2] Origami Design Secrets by Robert J. Lang
[3] http://origametry.net/combgeom/flatfold/flat.html
[4] Compliantmechanisms.byu.edu
[5] http://www.origamido.com/portfolio/american-alligator/
[6] https://www.flickr.com/photos/133610529@N05/26491343276/
